Le crépier

Le crépier psycho-rigide a une manie bien particulière. Lorsqu'il fait un lot de crêpes, chaque crêpe a une taille différente, et toujours exactement une face correctement cuite et une face brûlée. Il pose ses crêpes au fur et à mesure dans une assiette.

Dans un lot de n crêpes, il fait toujours : une crêpe de taille 1, une crêpe de taille 2, ... une crêpe de taille n-1 et une crêpe de taille n, mais il ne les fait pas forcément dans cet ordre.

Nous pouvons imaginer par exemple qu'après avoir fait 4 crêpes, son assiette contient cette pile, décrite à partir de la crêpe du dessus (Figure 1):

1. crêpe de taile 3, brûlée dessus
2. crêpe de taile 4, brûlée dessous
3. crêpe de taile 2, brûlée dessous
4. crêpe de taile 1, brûlée dessus

Une fois son lot de crêpes terminé, le travail n'est pas fini. Il faut impérativement ranger les crêpes par ordre de taille, la plus grande sur le dessous. Et il faut impérativement que la face brûlée ne soit pas visible (Figure 4).

Pour ranger ses crêpes, le crêpier ne s'autorise qu'une seule opération : prendre un tas de crêpes sur le dessus (autant qu'il veut, de 1 à toutes), et retourner ce tas. Par exemple, dans le cas decrit plus haut, il pourrait décider de retourner les 3 crêpes du dessus (Figure 2). Auquel cas, la configuration de la pile de crêpes serait alors (Figure 3) :

1. crêpe de taile 2, brûlée dessus
2. crêpe de taile 4, brûlée dessus
3. crêpe de taile 3, brûlée dessous
4. crêpe de taile 1, brûlée dessus

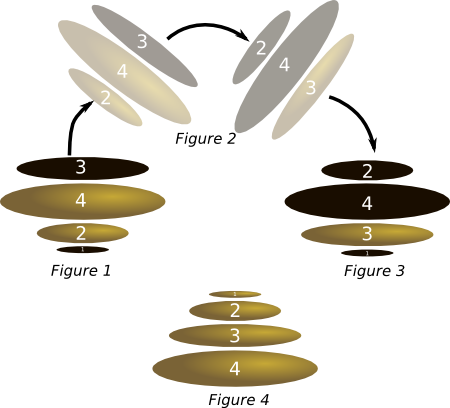
En faisant uniquement ce type d'opérations, plusieurs fois, il veut se retrouver dans cette configuration (Figure 4):

1. crêpe de taile 1, brûlée dessous
2. crêpe de taile 2, brûlée dessous
3. crêpe de taile 3, brûlée dessous
4. crêpe de taile 4, brûlée dessous

L'entrée du problème est la description du tas de crêpes, sous la forme d'une chaîne de caractères énumérant les crêpes à partir de celle du dessus. Chaque crêpe est décrite en donnant son diamètre (un nombre entier), puis la lettre I ou V, pour indiquer que la face brûlée est respectivement invisible ou visible. Le tas de crêpe initial serait alors décrit ainsi :

3V4I2I1V

Après avoir fait les retournements adéquats, la description de la pile devra être :

1I2I3I4I

Pour valider ce défi, vous devez indiquer au crêpier la liste des retournements de crêpes qu'il doit faire. Si vous pensez, par exemple (ce n'est pas la solution...) qu'il faut retourner les 3 crêpes du dessus, puis les 2 crêpes du dessus, puis les 4 crêpes, puis la crêpe du dessus, vous devez renvoyer la chaîne :

3241

Notez qu'avec ces retournements, la pile ne sera pas correcte, et on obtiendra :

1V3V2V4V

Voici le détail des opérations :

    3V4I2I1V
    retournement 3
    2V4V3I1V
    retournement 2
    4I2I3I1V
    retournement 4
    1I3V2V4V
    retournement 1
    1V3V2V4V
    

Pour n crêpes (il n'y en aura pas forcément 4, mais il n'y en aura jamais plus de 9), la solution que vous proposez ne devra pas contenir plus de 3n-2 opérations.