

Histoire
Pour son 3e travail, Eurysthée demanda à Hercule de capturer la biche aux pieds d'airain qui s'était enfuie de l'attelage d'Artémis.
La biche appartenant à Artémis, Hercule ne pouvait pas lui faire de mal sous peine de devoir essuyer la colère de la déesse. Il décida donc de l'épuiser en lui donnant la chasse dans les bois d'Oénoée. Toutefois, il dut veiller à ce qu'elle ne meure pas d'épuisement sans quoi il aurait alors dû affronter Artémis. Hercule estima que, pour avoir les meilleures chances de capturer la biche, il fallait que cette dernière traverse le bois en parcourant un nombre très précis de kilomètres. Ni plus, car elle aurait pu mourir d'épuisement, ni moins, car elle aurait eu encore suffisamment d'énergie pour échapper à Hercule au pied du mont Cyrénée.
Problème
Le bois dans lequel Hercule va s'aventurer est formé d'allées perpendiculaires les unes aux autres. Le bois se traverse en allant de la façade nord vers la façade sud. À chaque embranchement, on peut choisir d'aller à l'est ou à l'ouest. Hercule a relevé les positions des embranchements sous la forme d'une série de nombres. Vous devez indiquer à Hercule la liste des choix de direction qu'il doit réussir à imposer à la biche pour qu'elle ait parcouru, au sortir du bois, exactement le nombre de kilomètres souhaité, sachant de plus qu'elle ne revient jamais sur ses pas.Exemple
Voyons ce que cela donne avec une petite forêt. Hercule et la biche partent du point A, le point d'entrée unique situé au nord, et ils doivent sortir de la forêt par un des 8 points situés au sud de la forêt.
Pour repérer les positions des chemins, Hercule a procédé ainsi. Le point de départ est situé à l'abcisse 0. Un point qui est situé 1 km à l'est est à l'abscisse 1 et un point situé, par exemple 2 km à l'ouest du point de départ est à l'abscisse -2. Sur la figure suivante, on a relevé les abscisses de chacun des carrefours :
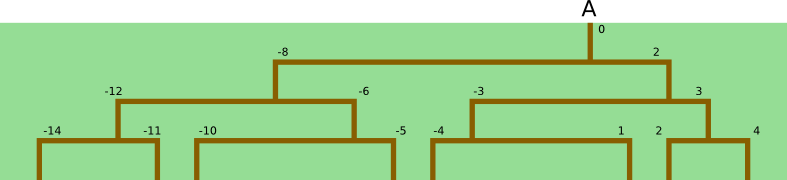
Puis, ces valeurs sont relevées en les lisant ligne par ligne, de haut en bas :
0, -8, 2, -12, -6, -3, 3, -14, -11, -10, -5, -4, 1, 2, 4
Enfin, chaque petit tronçon vertical a une longueur d'1km.
Imaginons qu'Hercule veuille traverser le bois en parcourant précisément 12 km. Il pourrait par exemple emprunter ce chemin :
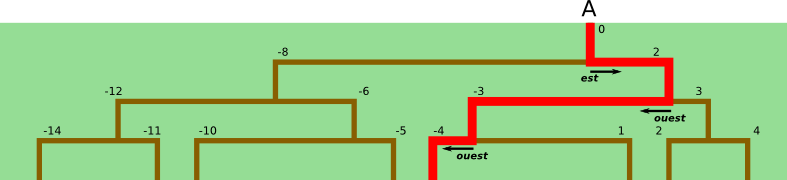
Dans ce cas, pour aider Hercule, il suffirait de lui dire, pour chaque carrefour,
s'il faut prendre à l'est (E) ou à l'ouest (O). Dans notre exemple, les indications à communiquer à Hercule
seraient simplement :
EOO
Testez votre code
Si Hercule avait fait ce relevé :0, -4, 9, -5, -1, 3, 12, -6, -4, -2, 0, 2, 9, 11, 13OEO.
En effet :
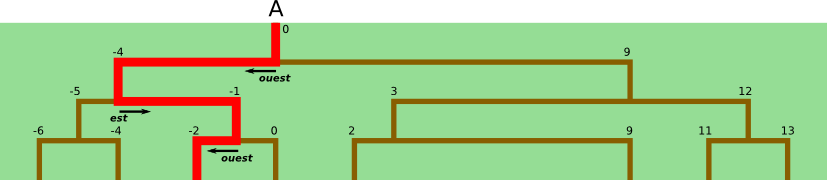
Notez au passage qu'il peut y avoir plusieurs solutions. Dans notre exemple, la réponse OEE
aurait aussi été convenable.
Défi
Voici le relevé qu'a fait Hercule :0,-879,308,-1198,-654,135,855,-1447,-1140,-859,-502,-56,263,544,1001,-1672, -1427,-1257,-1110,-950,-730,-514,-327,-204,-30,112,378,526,708,903,1084,-1707, -1632,-1509,-1409,-1302,-1234,-1171,-1099,-984,-842,-759,-648,-558,-477,-404, -313,-258,-202,-77,-26,62,152,302,390,483,592,646,754,874,985,1072,1191,-1747, -1675,-1642,-1594,-1526,-1475,-1437,-1394,-1347,-1292,-1254,-1214,-1188,-1137, -1104,-1031,-986,-929,-902,-841,-787,-743,-678,-643,-591,-545,-503,-460,-425, -367,-329,-306,-265,-232,-204,-155,-103,-75,-29,15,57,111,136,221,284,349,387, 420,469,501,525,595,615,651,709,790,837,890,974,1014,1061,1114,1170,1213,-1749, -1730,-1692,-1672,-1645,-1625,-1604,-1575,-1536,-1517,-1491,-1468,-1443,-1420, -1396,-1370,-1352,-1341,-1311,-1286,-1260,-1243,-1223,-1205,-1189,-1172,-1154, -1132,-1109,-1075,-1049,-1021,-990,-973,-947,-925,-903,-885,-862,-833,-792,-764, -747,-735,-692,-677,-651,-628,-604,-588,-560,-537,-518,-502,-475,-446,-435,-405, -370,-355,-336,-315,-307,-293,-272,-260,-248,-228,-209,-191,-162,-138,-117,-102, -82,-70,-53,-19,12,24,55,82,99,119,132,172,196,230,278,313,329,358,376,396,418, 439,455,472,485,508,522,539,565,596,612,636,649,677,691,729,777,806,822,849,879, 903,946,984,1001,1015,1055,1072,1101,1123,1153,1179,1199,1223,-1756,-1744,-1736, -1725,-1700,-1690,-1679,-1670,-1658,-1644,-1631,-1624,-1606,-1588,-1580,-1569, -1543,-1533,-1521,-1509,-1502,-1484,-1475,-1460,-1448,-1439,-1421,-1413,-1406, -1395,-1379,-1369,-1355,-1349,-1342,-1336,-1314,-1307,-1297,-1284,-1266,-1256, -1246,-1239,-1226,-1215,-1208,-1201,-1191,-1185,-1176,-1163,-1156,-1150,-1138, -1123,-1113,-1106,-1088,-1073,-1054,-1044,-1032,-1012,-996,-983,-974,-968,-962, -941,-930,-922,-915,-897,-889,-873,-864,-857,-853,-828,-796,-783,-774,-756,-748, -743,-736,-729,-698,-686,-681,-676,-660,-644,-629,-618,-606,-600,-590,-577,-568, -557,-543,-536,-522,-516,-505,-501,-487,-469,-452,-445,-438,-423,-415,-402,-385, -366,-357,-348,-337,-329,-322,-313,-309,-300,-294,-286,-276,-271,-265,-259,-250, -243,-236,-226,-214,-208,-194,-190,-179,-157,-149,-131,-124,-116,-107,-96,-84, -75,-71,-66,-61,-46,-23,-9,2,14,22,35,52,63,71,91,98,102,115,123,131,138,170, 179,195,202,217,241,266,281,305,314,326,336,356,362,375,383,394,402,417,424,432, 441,447,457,469,473,483,488,499,511,518,528,536,542,555,572,580,603,607,624,631, 637,646,653,665,678,689,695,715,760,774,791,802,810,820,833,842,856,872,883,902, 919,933,947,966,986,995,1005,1011,1022,1033,1056,1071,1087,1098,1102,1109,1128, 1145,1157,1166,1182,1197,1206,1216,1224,-1758,-1752,-1750,-1741,-1737,-1734, -1728,-1710,-1701,-1699,-1694,-1688,-1680,-1678,-1671,-1669,-1667,-1648,-1646, -1639,-1634,-1627,-1625,-1622,-1615,-1593,-1591,-1586,-1582,-1575,-1571,-1568, -1547,-1539,-1537,-1529,-1522,-1513,-1511,-1508,-1503,-1494,-1485,-1482,-1476, -1471,-1462,-1452,-1449,-1444,-1442,-1437,-1422,-1420,-1414,-1411,-1407,-1402, -1397,-1394,-1380,-1377,-1375,-1368,-1364,-1354,-1351,-1347,-1345,-1341,-1338, -1334,-1327,-1313,-1308,-1302,-1298,-1294,-1290,-1279,-1276,-1265,-1259,-1255, -1250,-1245,-1243,-1233,-1230,-1225,-1216,-1213,-1211,-1206,-1204,-1199,-1193, -1188,-1186,-1184,-1179,-1172,-1169,-1162,-1159,-1155,-1152,-1142,-1140,-1136, -1130,-1118,-1116,-1111,-1107,-1096,-1094,-1077,-1075,-1071,-1062,-1053,-1050, -1041,-1033,-1024,-1017,-1011,-997,-994,-992,-979,-976,-972,-969,-967,-964,-961, -949,-938,-931,-927,-923,-918,-916,-914,-900,-896,-894,-876,-874,-872,-870,-862, -858,-856,-854,-852,-830,-816,-800,-792,-788,-780,-776,-773,-758,-755,-752,-747, -745,-741,-737,-735,-730,-725,-700,-694,-688,-684,-682,-679,-677,-675,-663,-655, -646,-640,-638,-626,-619,-616,-608,-603,-601,-596,-591,-583,-578,-575,-570,-565, -558,-552,-545,-542,-538,-532,-529,-521,-517,-509,-506,-504,-502,-499,-494,-480, -471,-462,-453,-451,-446,-443,-440,-428,-425,-421,-416,-413,-404,-392,-387,-377, -370,-365,-359,-354,-350,-347,-340,-332,-330,-328,-326,-320,-318,-312,-310,-307, -301,-298,-296,-293,-288,-281,-278,-275,-273,-270,-266,-264,-262,-258,-252,-246, -244,-242,-237,-235,-233,-222,-219,-213,-210,-201,-195,-193,-191,-189,-182,-164, -158,-156,-151,-147,-143,-130,-126,-120,-118,-113,-109,-104,-100,-95,-85,-82, -80,-74,-72,-70,-67,-65,-62,-60,-50,-40,-31,-20,-14,-2,1,6,10,15,18,25,34,36,40, 59,61,68,70,73,90,92,96,99,101,107,111,116,121,124,129,133,137,143,169,172,177, 180,194,197,200,203,213,220,237,242,253,270,278,288,301,306,312,319,325,327,335, 338,343,357,361,364,374,376,382,385,393,396,398,403,415,419,423,425,431,433,440, 442,446,448,456,461,466,470,472,474,479,484,486,490,497,500,507,514,516,522,526, 531,533,538,540,547,550,561,565,574,577,583,600,604,606,616,621,625,630,632,634, 638,644,649,651,657,664,670,674,685,687,690,692,696,704,721,751,765,771,782,784, 797,800,804,807,813,817,824,832,834,841,853,855,857,865,874,878,893,900,904,907, 922,925,935,945,948,965,972,984,989,994,996,1001,1006,1009,1016,1021,1026,1031, 1037,1050,1059,1068,1076,1084,1088,1097,1099,1101,1103,1107,1110,1124,1131,1143, 1151,1154,1159,1163,1171,1181,1183,1193,1203,1205,1207,1213,1217,1222,1225