Histoire

Pour son 3^e travail, Eurysthée demanda à Hercule de capturer la biche aux pieds d'airain qui s'était enfuie de l'attelage d'Artémis.

La difficulté pour Hercule était de capturer la biche sans la blesser, sous peine d'essuyer la colère d'Artémis. Il decida donc de l'épuiser en la poursuivant dans les bois d'Oénoée.

Son plan était clair : il commença par aménager les carrefours afin que la biche, à chaque embranchement, n'ait qu'un seul choix de parcours. Il construisit un plan qui ressemblait un peu à celui-ci, encore que le vrai plan était beaucoup plus grand :

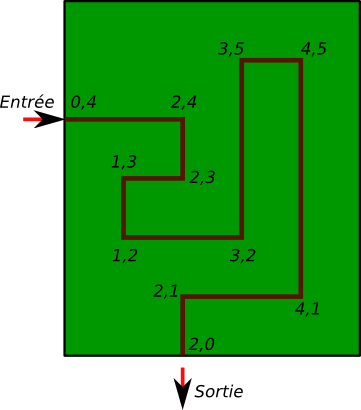
Les chemins étaient tous parfaitement orthogonaux, direction Nord-Sud ou Est-Ouest. Puis il nota les positions des carrefours, dans l'ordre où la biche devait les parcourir. Dans l'exemple qui précède, il aurait noté les coordonnées de tous les points ainsi : (0,4), (2,4), (2,3), (1,3), (1,2), (3,2), (3,5), (4,5), (4,1), (2,1), (2,0)

Enfin, il dût choisir ses chaussures. Hercule étant un athlète très méthodique, sa paire de chaussures devait être choisie en fonction de la distance précise qu'il aurait à parcourir.

Problème

Dans l'exemple qui précède, en suivant le parcours indiqué par les positions des carrefours, notées en kilomètres, Hercule aurait parcouru 18 kilomètres, ce que l'on peut voir sur le dessin, mais aussi calculer à partir du relevé de coordonnées.

Le bois d'Oénoée était en réalité beaucoup plus grand que ce qui est indiqué précédemment. L'entrée du problème est le relevé des positions des carrefours, tous les nombres ayant été mis à la suite, sans les parenthèses, et les valeurs étant données en kilomètres. Aide Hercule en calculant pour lui la distance qu'il aura à parcourir dans le bois, à la poursuite de la biche.