Histoire

Après avoir refusé de sacrifier à Poséidon le taureau qui lui avait été offert, Minos le cacha dans son troupeau. Mais Poséidon, en colère, rendit le taureau tellement fou que celui-ci ravageait les villages de Crète. Pour son 7^e travail, Eurysthée demanda à Hercule de capturer ce taureau.

Vous connaissez sans doute l'histoire du Minotaure, la créature mi-homme, mi-taureau cachée par Minos dans un labyrinthe construit par Dédale. Il est moins connu que Minos et Dédale avaient fait leurs classes avec le taureau de Crète, non pas réfugié dans une caverne comme on le lit souvent, mais dans un labyrinthe, comme l'était le Minotaure.

Le taureau avait ainsi l'habitude de se réfugier dans une des pièces du labyrinthe, que Dédale seul pouvait retrouver tant le chemin qui y menait était compliqué (nul ne sait comment le taureau, de son côté, y parvenait).

Dédale, moqueur, expliqua à Hercule qu'il y avait une méthode pour trouver le chemin vers le taureau :
«C'est simple, avec la lettre A, tu avances de 10 mètres, avec la lettre G, tu tournes d'un quart de tour sur ta gauche, et avec la lettre D, tu tournes d'un quart de tour sur ta droite.
Il suffit que tu connaisses la bonne série de A, de G et de D et tu pourras retrouver le taureau. Et justement, il y a une méthode pour construire cette série. Écoute-bien : Tu pars de la séquence DG puis tu remplaces, dans cette séquence :

• D par DAGAGA
• G par GADADA
• A par AA (je sais qu'il n'y a pas de A dans la série DG mais attends...)

En partant de la séquence DG, tu auras donc :

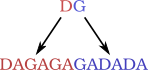
Puis tu recommences une deuxième fois, avec les mêmes règles. Et tu obtiens :

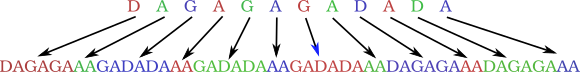
Recommence ainsi jusqu'à la dixième fois, et tu auras le chemin vers le taureau, depuis l'entrée du labyrinthe, si tu regardes vers le nord.

Défi

Le chemin que l'on trouve par ce moyen est très long. Il serait plus rapide de localiser directement le taureau dans le labyrinthe. Aidez Hercule à localiser le taureau en lui indiquant à quelle distance il se trouve au nord et à l'est.

Testez votre code

Si plutôt que de les appliquer 10 fois, il avait suffit d'appliquer les règles 2 fois, le chemin vers le taureau aurait été (comme nous venons de le voir) : DAGAGAAAGADADAAAGADADAAAGADADAAADAGAGAAADAGAGAAA

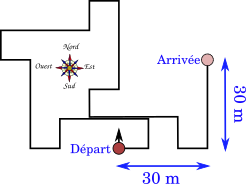
En suivant ce chemin, Hercule aurait donc parcouru 30 mètres vers le nord et 30 mètres vers l'est.

Dans ce cas, il aurait suffit de répondre 30,30