Nous proposons ici une variante d'un problème ancien (très ancien...), qui a donné naissance à plusieus problèmes de décimation, dont le fameux Catching the mice d'Ernest Dudeney.
Dans la variante proposée ici, le matou va faire son repas avec N souris (N est donné en entrée). Certaines souris sont blanches et d'autres sont grises. Les souris sont placées en cercle. Le matou décide de manger une souris toutes les k souris (k est donné en entrée).
Supposons que N = 6 et k = 3 (figure a). Il commence à compter sur la souris 1 : 1, 2, 3 et il croque la souris numéro 4 (figure b). Il compte à nouveau : 1, 2, 3 (en désignant les souris suivantes). Puis il croque la souris suivante (figure c). Il continue à compter : 1, 2, 3 (en désignant les souris 3, 5, 6) et croque la souris suivante (figure d). Il compte à nouveau : 1, 2, 3 (en désignant les souris 3, 5, 6) et croque la souris suivante (la 3, figure e). Il continue : 1, 2, 3 (en désignant les souris 5, 6, 5) et croque la souris 6 (figure f). Enfin il compte 1, 2, 3 (en designant 3 fois la souris restante), puis croque la dernière souris (la numéro 5, figure g).
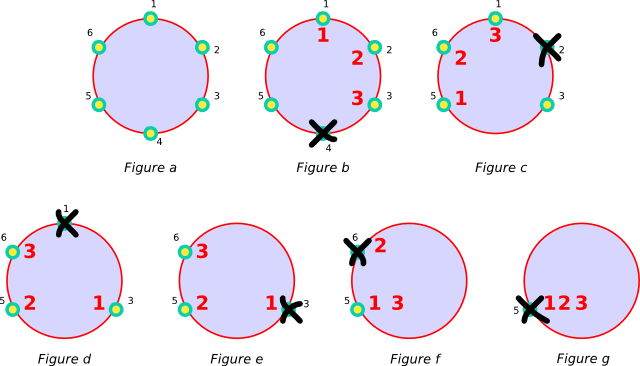
Dans l'ordre, le matou aura donc croqué :
- en numéro 1, la souris qui était en position 4,
- en numéro 2, la souris qui était en position 2,
- en numéro 3, la souris qui était en position 1,
- en numéro 4, la souris qui était en position 3,
- en numéro 5, la souris qui était en position 6,
- en numéro 6, la souris qui était en position 5.
Or notre matou est passioné par les nombres, il souhaite croquer en numéro i une souris blanche si et seulement si i est premier.
Dans l'exemple qui précède (N = 6 et k = 3), les souris blanches devront donc être en positions 2, 1, 6 (car elles seront croquées respectivement en 2e, en 3e et en 5e, et 2, 3 et 5 sont premiers). Rappelons que 1 n'est pas premier.
Des valeurs des N et k sont données en entrée du problème. Vous devez fournir en réponse la séquence des positions dans lesquelles il faut placer les souris blanche. Peu importe l'ordre des éléments dans votre séquence. (pour N=6 et k=3, vous pourriez par exemple répondre 1, 2, 6).